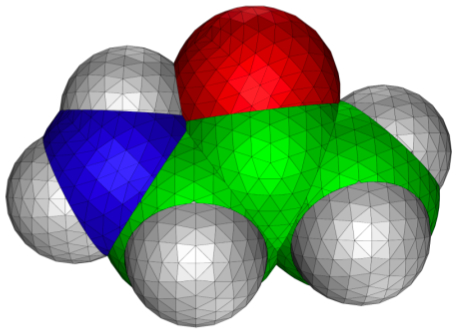
Figure 3.7. Contour plot of the RHF/6-31G(d) electrostatic potential and 0.002 au isodensity surface of (a) CH
3COO
-, (b) HF, and (c) F
2. The maximum/minimum contour values are, respectively, 0.5/0.025; 0.1/0.005; and 0.005/0.00025 au respectively. Blue corresponds to a negative potential. In each case the outer-most contour looks like the corresponding contour in the electrostatic potential due to a charge, dipole, and quadrupole, respectively.
From
Molecular Modeling Basics CRC Press, May 2010.
This figure makes 3 points:
1. It shows what the electrostatic potential of a charge, dipole, and quadrupole looks like.
2. It show the relative strengths of the electrostatic potentials due to a charge, dipole, and quadrupole.
3. It shows that the electrostatic potential of a charge, dipole, and quadrupole deviates significantly from the actual electrostatic potential near the molecular surface.
Here is a screencast showing how I made Figure 3.7a. (If I were to do it over I would have chosen red for negative and blue for positive... oh, well.)
Here is an interactive version of the figure. Click on the picture to load it. Remember it's Jmol so you can rotate it and zoom as you like (Mac users: this works best with Safari).

Figure 3.7. The RHF/6-31G(d) electrostatic potentials of acetate, HF and F
2.
Click on the picture for an interactive version
See these two posts (
here and
here) on how to make plots like that with Jmol. From a Jmol perspective the only new thing is that I show two isosurfaces simulateneously. This is done by loading the file twice to create two "frames" that Jmol can display simultaneously. You can find the script file with all the commands
here, but the general syntax is:
load files file1.xyz file2.xyz
frame 1.1; isosurface surf1 plane {0 0 0 0} contour 40 color range -0.05 0.05 "potential.cube.gz"
frame 2.1; isosurface surf2 0.002 "density.cube.gz" Even though you want a 2D contour plot of the potential, it is necessary to make a 3D cube file. Because I use unusually low cutoffs to show the outer contours, I had to trick MacMolPlt into making a bigger grid. I show how on the screencast below.